Generalised suffix tree
In computer science, a generalised suffix tree is a suffix tree for a set of strings. Given the set of strings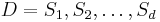 
of total length 
, it is a Patricia tree containing all suffixes of the strings. It is mostly used in bioinformatics.[1]
Contents |
Functionality
It can be built in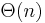 
time and space, and can be used to find all 
occurrences of a string 
of length 
in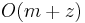 
time, which is asymptotically optimal (assuming the size of the alphabet is constant, see [2] page 119).
When constructing such a tree, each string should be padded with a unique out-of-alphabet marker symbol (or string) to ensure no suffix is a substring of another, guaranteeing each suffix is represented by a unique leaf node.
Algorithms for constructing a GST include Ukkonen's algorithm and McCreight's algorithm.
Example
A suffix tree for the strings ABAB and BABA is shown in a figure above. They are padded with the unique terminator strings $0 and $1. The numbers in the leaf nodes are string number and starting position. Notice how a left to right traversal of the leaf nodes corresponds to the sorted order of the suffixes. The terminators might be strings or unique single symbols. Edges on $ from the root are left out in this example.
Alternatives
An alternative to building a generalised suffix tree is to concatenate the strings, and build a regular suffix tree or suffix array for the resulting string. When hits are evaluated after a search, global positions are mapped into documents and local positions with some algorithm and/or data structure, such as a binary search in the starting/ending positions of the documents.
References
- ^ Lucas Chi Kwong Hui (1992). "Color Set Size Problem with Applications to String Matching". Combinatorial Pattern Matching, Lecture Notes in Computer Science, 644.. pp. 230–243. http://www.springerlink.com/content/y565487707522555/.
- ^ Paul Bieganski, John Riedl, John Carlis, and Ernest F. Retzel (1994). "Generalized Suffix Trees for Biological Sequence Data". Biotechnology Computing, Proceedings of the Twenty-Seventh Hawaii International Conference on.. pp. 35–44. http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=323593.
- ^ Gusfield, Dan (1999) [1997]. Algorithms on Strings, Trees and Sequences: Computer Science and Computational Biology. USA: Cambridge University Press. ISBN 0-521-58519-8.